Statistical Process Control (SPC)?
SPC is controlling the process variation by using statistical techniques. Statistical techniques such as Control charts and histograms are used to analyze the process & achieve & maintain a state of statistical control to get a product having no defect.
What is Statistics?
It is information derived from the sample data to estimate the process. It includes collecting of data, data analysis, data interpretation & taking actions based on the analysis.
What is Statistical Control?
The condition describes a process from which all special causes of variations have been eliminated & only a common cause exists.
What is a Process?
The process is converting input into output by using resources i.e. man, machine, material & method. Also during this conversion value is added.
What is Variation?
The inevitable difference among the individual outputs of a process is called variation. As we know no two things can be produced the same in the world. In other words, we can say dissimilarity between two products for the same dimension is called variation.
Types of Variation:
1. Common Cause Variation
2. Special Cause Variation
Common Cause Variation:
The source of variation that affects all the individual values of the process & is inherent in the process & can not be eliminated. It is common to all value/observation of the process in all periods. As it is within the process it can be called inherent variation.
It is also called white noise. Some examples of common cause variation are machine parts wear, and tool worn out.
Special Cause Variation:
Source of variation that is intermittent, unpredictable & unstable. This type of source of variation can be identified & eliminated permanently. It is a sudden type of variation.
These are not common to all periods. In such types of variations, statistics can not be applied. It is also called black noise. Machine and tool breakdowns are examples of special causes of variation.
Process Stability:
The process will be stable when the process is in control & variation is constant for time.
What is Mean:
The mean of ‘n’ values is the sum of all the values divided by ‘n’.
X = (X1+X2+X3+X4+ …………+Xn)/n
What is Range:
The difference between the largest value & smallest value of a set of numbers.
R = X max – X min
What is Spread ( Standard Variation):
Standard deviation is the average distance between the individual numbers and the mean.
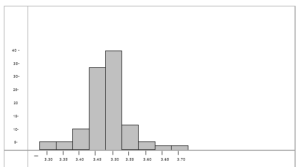
Histogram:
It is a tool used to determine the normal distribution of a process. Histogram provide a graphical view of the distribution of the values. It shows graphically the variation of a process. The figure illustrates frequency in the form of a pole. The frequency data obtained from measurements display a peak around a certain value. The variation of quality characteristics is called distribution.
What are the Population and sample?
The entire set of items is called the Population. The small number of items taken from the population is called the Sample. The number of samples taken to make this judgment is called a Sample size.
How to Make a Histogram?
- Collect the data.
- Determine the cell width.
- Group the data as per the cell width.
- Using a graph, plot the frequency of occurrence on the Y-axis & specification limit on the X-axis.
- Analyze the graph for normal distribution.
- The abnormal distribution indicates the availability of special causes.
Interpretations for the Histogram:
1. Check the specification – It represents the acceptance or the rejection.
2. Check the width – It represents the capability.
3. Check the shape – It represents the predictability
Steps in making the Histogram:
1. Collect the data:

2. Count the number of readings, N=100
3. Find the maximum value Xmax & minimum value Xmin.
4. Find out the Range. R= Xmax – Xmin
5. Find out the class interval,h=R/K
Where h is the class interval
R is Range
K is a number of classes.

6. From the above table K=10
7. Class interval h=0.38/10= 0.038
h=0.40 (rounded off) Consider value of h = 0.5 ( for easy calculation)
8. Cell width = Class interval/2= 0.5/2= 0.025
9. Draw a frequency diagram as shown below:
Frequency Table :

Control Charts for Variable:
Control Charts for variables are a powerful tool that can be used when measurements from a process are variable. The performance of a process can be analyzed with variables and improvement can be possible even if all the values are within the specification limit.
How to make X bar – R chart :
X bar- R chart is developed to measure particular characteristics of the process output. X bar- R chart explains process data in terms of both its spread & its location.
How to collect data :
Data are collected in a small subgroup of constant size ( 2 to 5 consecutive pieces). Subgroups are taken periodically. Also sample size should remain the same for all subgroups.
What is Subgroup Size :
Subgroup size should be chosen so that opportunities for variation among the units within a subgroup are small.
Subgroup Frequency:
It is the frequency of taking subgroups (samples) during the SPC study. During the initial process, study subgroups are taken at short intervals. But during normal production, the frequency can be increased.
Number of Subgroups:
Normally we should take 20 or more subgroups containing 100 or more readings. We should take subgroups such as the major source of variation that can be captured.
Plotting the Average & Range on the Control Charts:
Plot the average & range on their respective charts. Connect the points with lines to visualize patterns & trends. Check the plot points & verify that calculations & points are correct. Ensure that the plot points for the corresponding X and R are vertically in line.
Calculate Control Limits:
R= (R1+R2+R3+ +Rn)/K
X= (X1+X2+X3+ +Xn)/K where K is a number of subgroups.
R1 is the range of the 1st subgroup.
X1 is the average of the 1st subgroup.
Setup Control Charts:
X & R charts are normally drawn with X chart above the Range chart and the value of X & R will be vertical scale.
Average(X)= (X1+X2+X3+ +Xn)/n
where n is the subgroup sample size.
Range, R= Xmax – Xmin
Select the scale of the control chart: For the X chart generally, the scale should be double the range.
Similar to the R chart it should be double the range.
For the R chart, UCLr = D4 x R LCLr = D3 x R
For X chart, UCLx = X + A2 R LCLx = X – A2 R
where D4, D3 & A2 are constant as per sample size.
Draw the Range average and process average as solid horizontal lines & control limits are as dashed horizontal lines.
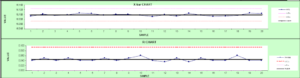
Interpretation of the Control Charts :
We should analyze the Range chart first. The data points are compared with control limits for the points out of control & trends.
For Range chart :
A) The points out of control limits are the evidence of non-control of the process. So a special cause is there in the process. A point out-of-control limit is due to
1) Piece-to-piece variation has been increased or decreased.
2) MSA has been changed.
B) The presence of unusual patterns/trends even if all ranges are within control limits can be evidence of process spread due to special cause.
C) Runs
1) 7 points in a row on one side of the average indicate the process is not normally distributed & there is a shift in the process average.
2) 7 points in a row that are constantly increasing or decreasing.
D) The presence of the cycle in the chart indicates that the special cause is due to the machine setup, wear of the machine and material variation etc.
Find & address the special cause:
For each indication of the special cause in Range data, conduct an analysis of the operation of the process to determine the cause & improve the process.
Analyzing the average chart:
When ranges are in statistical control, the process spread is considered stable. The average can be analyzed to see if the process location changes over time. The points out of control limits indicate that,
1. Shift in process.
2. Plot points are in error.
Find and eliminate the special cause & then recalculate the control limit after eliminating the special cause.
Standard deviation formula:
Standard Deviation (Sigma) = R/d2
where R is the average of the subgroup range
d2 is constantly varying the sample size.
Process capability can be described in terms of the distance of the process average from the specification limit in standard deviation unit Z
For Unilateral Tolerance:
Z= (USL – X bar)/ Std deviation Z = ( X bar – LSL) / Std deviation
For Bilateral Tolerance:
Zusl = (USL – Xbar) / Std deviation Zlsl = (Xbar – LSL) / Std deviation
The value of Z min can be converted to the capability index,
Cpk = Zmin/3 = min of (USL – Xbar)/ 3 sigma & (Xbar – LSL)/3 sigma
Process Capability Index:
Cpk = Min ( (USL – X bar)/3 Sigma & (X bar – LSL)/3 Sigma)
Process Capability :
It is the measurement of the inherent variation of the process when it is in stable condition for process specification.
Cp = (USL – LSL) / 6 sigma
SPC Format :



very nice explanation