What is a histogram?
The histogram is a graphical view of variation in a set of data. The pictorial nature of the histogram enables us to see patterns easily. However, it is complicated to see the pattern in a simple table of numbers. It is a tool used to determine the normal distribution of a process.
A French statistician A M Guerry first developed a histogram in 1833. Guerry introduced a new kind of bar graph to describe his analysis of crime data.
Key concepts about histograms:
① Values in a set of data usually show variation: Variation is everywhere. It is inevitable in the output of any process. It is impossible to keep all factors in a constant state all the time.
② Variation always shows a pattern: Different factors will have different variations, but there is always some pattern to the variation. These patterns of variation in data are called distributions.
There are three important characteristics of a histogram :
ⓐ It’s center
ⓑ Its width
ⓒ Its shape
③ Pattern of variation is difficult to see in a simple table of numbers
④ Pattern of variation is easier to see when data are summarized pictorially in a histogram.
How to use and interpret a histogram?
Identifying and explaining the pattern of variation: The goal of the analysis of a histogram is to :
- Identify and classify the pattern of variation
- Develop a reasonable and relevant explanation for the pattern.
You may like to know about Stratification in 7 QC Tools.
You may like to know about Scatter diagram in 7QC Tools.
How many types of histograms?
① Bell-shaped Distribution :
A symmetrical shape with a peak in the middle of the range of the data. This is the normal distribution of data from a process. Deviation from this bell shape may indicate the presence of outside influence.

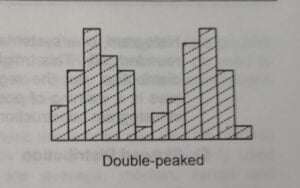
② Double Peaked Distribution :
A significant drop in the middle of the range of data with a peak on either side. This pattern normally combines two bell-shaped distributions and suggests that two distinct processes are at work.
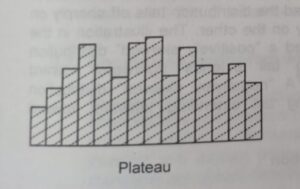
③ Plateau Distribution :
A flat top with no distinct peak and a slight tail on either side. This pattern is likely to be the result of many different bell-shaped distributions with centers spread evenly throughout the range of the data.
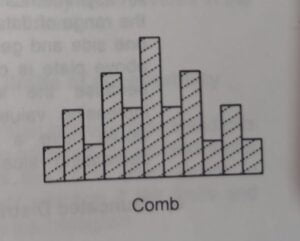
④ Comb Distribution :
High and low values alternate regularly. This pattern typically indicates measurement error, errors in the way the data were grouped to construct the histogram. The presence of alternating high and low is a warning of possible errors in data collection.
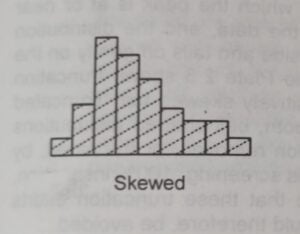
⑤ Skewed Distribution :
An unsymmetrical shape in which the peak is off-center in the range of data and the distribution tails off sharply on one side and gently on another side. This may be positively skewed or negatively skewed as per rightward or leftward respectively.
⑥ Truncated Distribution :
An unsymmetrical shape in which the peak is at or near the edge of the range of data and the distribution ends on one side and tail off gently on the other.

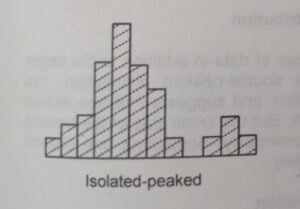
⑦ Isolated peaked Distribution :
A small, separate group of data in addition to the larger distribution. It is like the double-peaked distribution. However, the small size of the second peak indicates an abnormality.
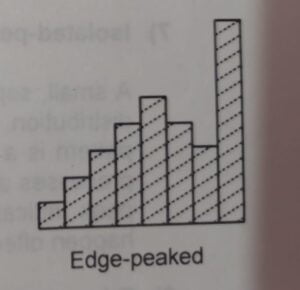
⑧Edge peaked Distribution:
A large peak is attached to an otherwise smooth distribution. This shape occurs when the extended tail of the smooth distribution has been cut off and lumped into a single category at the edge of the range of the data.
Precautions in the Interpretation of Histogram
There are 3 main precautions during interpreting histograms.
- Data should be from the current and typical conditions of the process.
- The sample size should be large.
- Interpretation of the histogram must be confirmed through analysis & observation of the process.
Use of Histogram in Quality Control:
- Identifying the root cause
- The histogram is a simple but powerful analytical tool that helps us to understand the process and develop reasonable, fact-based theories about the root cause of the problems.
- To check the process performance
How to make a histogram?
Below are the steps in constructing a Histogram:
Step 1: On the raw data table, determine the high value, low value and range.
Step 2: Decide on the number of cells
| Number of Data Points | Recommended Number of Cells |
|---|---|
| 20 – 50 | 6 |
| 51 – 100 | 7 |
| 101 – 200 | 8 |
| 201 – 500 | 9 |
| 501 – 1000 | 10 |
| Over 1000 | 11 – 20 |
Step 3: Calculate the approximate cell width
Step 4: Round the cell width to a convenient number
Step 5: Construct the cells by listing the cell boundaries
Step 6: Tally the number of data points in each cell
Step 7: Draw and label the horizontal axis
Step 8: Draw and label the vertical axis
Step 9: Draw in the bars to represent the number of data points in each cell.
Step 10: Title the chart, indicate the total number of data points and show nominal values and limits.
Step 11: Identify and classify the pattern of variation
Step 12: Develop a reasonable and relevant explanation for the pattern
You may like more details about SPC, Control Chart and Histogram.


Thankyou for sharing the information with us.